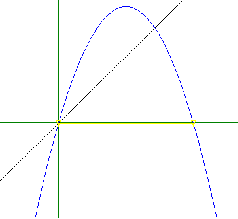
Объект изучения - квадратичное отображение x_n+1=rx_n(1-x_n). Это одномерное необратимое отображение с единственным управляющим параметром появилось в задачах популяционной биологии, но с развитием нелинейной динамики и особенно концепции динамического хаоса приобрело статус эталонного простого (минимальной размерности) объекта с хаотической динамикой. 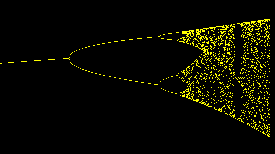Программа иллюстрирует графические методы изучения колебательных режимов в одномерных отображениях (диаграмма Ламерея) и способы представления информации (фазовые портреты, временные реализации, бассейн притяжения аттрактора, бифуркационная диаграмма), сценарий перехода к хаосу через каскад бифуркаций удвоения периода и определение одной из универсальных констант Фейгенбаума.

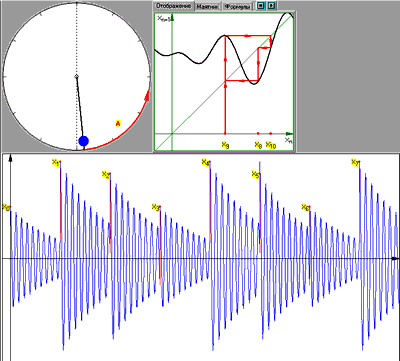
На примере одномерного нелинейного отображения (модели нелинейного маятника под импульсным внешним воздействием) иллюстрируются бифуркации, гистерезис, динами-ческий хаос, мультистабильность и другие феномены, присущие нелинейным колеба-тельным системам.

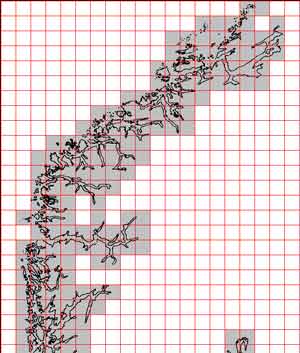
Проводится знакомство с фракталами и понятием фрактальной размерности - емкости. Фракталы - геометрические объекты (линии, поверхности, тела), имеющие сильно изрезанную форму и обладающими самоподобием. Изрезанность означает, что, уменьшая масштаб рассмотрения, мы будем видеть все более и более мелкие детали. Самоподобие означает, что фрактал одинаково устроен в широком диапазоне масштабов: мелкие детали, видные на малых масштабах подобны более крупным, видимым на больших масштабах. В программе емкость рассчитывается методом, непосредственно опирающимся на ее определение, т.е. путем покрытия исследуемого множества кубами все меньшего размера. Представлены примеры реальных объектов (побережье Норвегии), имеющих фрактальные свойства.

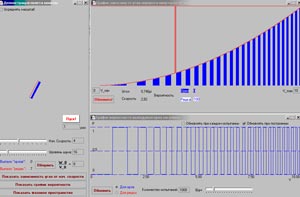
Иллюстрируется возможность описания одного и того же реального объекта различными по своей сути и форме моделями, динамическими и вероятностными. Каждая из них имеет право на существование, полезна для достижения определенных целей. Это лишний раз показывает условность ярлыков "динамическая система" или "случайная величина" в приложении к реальным объектам и ситуациям. Международный символ случайности - монета, падающая с вращением, при определенных условиях вполне предсказуема. Ее целесообразно рассматривать с позиций концепции частичной детерминированности. Программа имитирует процесс подбрасывания монеты с различными начальными условиями и при различных уровнях неточности в их задании.

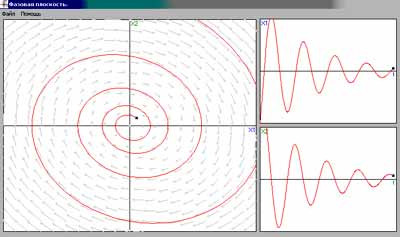
Наглядно иллюстрируются поля скоростей, фазовые траектории и временные реализации для эталонных осцилляторов и произвольных заданных пользователем двухмерных систем с непрерывным временем.

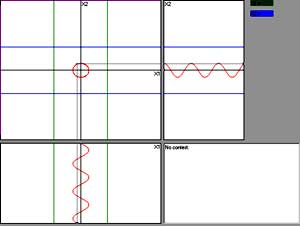
Иллюстрируются траектории на фазовой плоскости и временные реализации отдельных переменных, заданные формулами или таблицами.

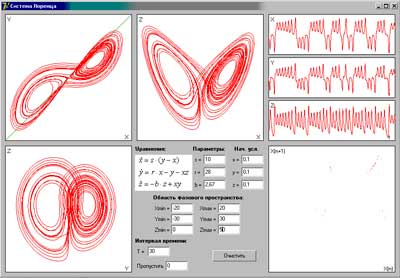
Изучается динамика эталонной хаотической системы (системы Лоренца) при различных значениях управляющих параметров. Представлены временные реализации, проекции фазовых траекторий, сечение Пуанкаре.