Динамическое моделирование
Приступая к созданию модели, очень важно определиться с претензиями на ее прогностические возможности. Сделанный выбор определяет вид требуемого математического аппарата. Если претензии на точный однозначный прогноз будущих состояний по начальному отсутствуют, традиционно используют вероятностный подход. При этом все или часть величин, описывающих объект моделирования, объявляются случайными, т.е. принципиально непредсказуемыми, стохастическими. Для такого "приговора" могут быть различные основания, но если он "подписан", используется аппарат теории вероятностей и математической статистики.
Альтернативный вероятностному динамический подход опирается на концепцию детерминизма. Детерминизм - учение о закономерности и причинной обусловленности всех явлений природы и общества. Для реализации этого подхода требуется математический аппарат, обеспечивающий однозначный прогноз, классическим (но не единственным) образцом которого являются дифференциальные уравнения.
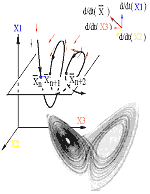
Итак, в основе динамического подхода лежит представление о том, что все будущее поведение объекта однозначно определяется его состоянием (x) в начальный момент времени. Состоянием (вектором состояния) называют совокупность D величин: x=(x1, x2, ..., xD), где D - размерность описания. Правило, которым однозначно определяется эволюция объекта из начального состояния x(t0), называют оператором эволюции Фt. Состояние в любой последующий момент времени t0+t находится как x(t0+t)=Фt(x(t0)). Оператор эволюции задается уравнениями, отображениями, матрицами, графами и любыми другими способами, обеспечивающими выполнение условия однозначности прогноза. Всю описанную модельную конструкцию называют динамической системой (т.к. терминология в этой области знаний еще не устоялась в эти слова вкладывают различный смысл, с чем можно познакомиться в разделе 2.1 книги).
|
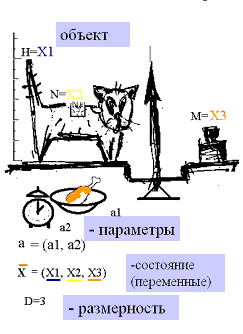
В качестве примера в качестве объекта моделирования возьмем обыкновенную кошку. Если цель моделирования - описание эволюции здоровья животного, в качестве динамических переменных можно предложить ее массу M=x3, рост H=x2 и густоту шерсти - число "шерстинок" на единицу площади N=x1. Совокупность x=(x1, x2, x3) - вектор состояния; при этом размерность описания D = 3. Мы не можем здесь предложить выражение для оператора эволюции, но очевидно, что развитие кошки будет зависеть, например, от ее питания (a1 - масса пищи в суточном рационе в кг/день) и условий существования (a2 - длительности прогулок на свежем воздухе в час/день). В отличие от динамических переменных, величины, a1, a2 и подобные им, которые могут поддерживаться постоянными или целенаправленно регулироваться, называют параметрами. Параметрами динамических систем являются коэффициенты в уравнениях эволюции.
|
Разделение характеризующих величин на переменные и параметры диктуется условиями задачи моделирования. Если бы целью моделирования упомянутой кошки было описание ее механического перемещения в пространстве (а не здоровья, как ранее) разумно было быв качестве переменных выбрать координаты ее центра масс (x1=x, x2=y, x3=z) и углы поворота продольной оси относительно осей координат (x4=α, x5=β, x6=γ), а массу животного M, его "пушистость" N и геометрические размеры H, которые не изменятся за время прыжка, но существенно влияют на полет - в качестве параметров (a1=M, a2=>N, a3=H). Обратите внимание, что величины, при одной цели моделирования служившие динамическими переменными, при другой - стали играть роль параметров.
|
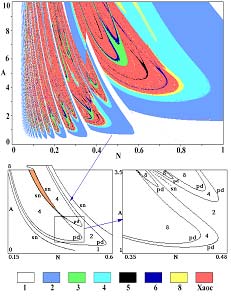
Динамическое моделирование располагает очень широкими наглядного возможностями представления информации, такими например, как представленные на рисунках портреты в пространстве состояний (фазовые портреты), структуры разбиений пространства параметров на области существования различных вариантов движений и т.д.
|