1. Analysis of complex signals and reconstruction of model equations from time
series of experimentally observed quantities.
|
|---|
Digital signal processing is widely used in modern measuring devices. Experimentally
observed quantities are represented by means of analog-to-digital converters (ADC)
in the form of discrete sequences of values measured at subsequent time instants (time series).
Such data are "understood" by a computer which processes them and generates a final result.
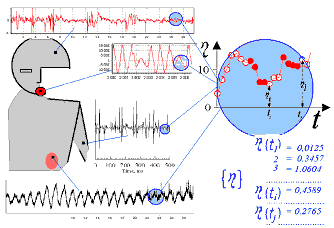 As a rule, real-world signals are complex (often even chaotic), nonstationary, and noisy. The examples
are the recordings from human being obtained with the use of diagnostic devices (see the left Figure:
electric signals from scalp and muscles - electroencephalogram and electromyogram, pressure recordings
from throat and nephron). Processing of such signals requires development and employment of different
methods and tricks (technologies) some of which are classical and used for a long time, while others
appeared recently and currently gain their popularity. For definiteness, one can systematize them
according to their relation to the following two approaches. Observed
time realizations can be analyzed directly, e.g., by computation of classical Fourier spectra
(decomposition into sinusoidal functions) or modern wavelet spectra, by estimation of probability
distribution, mean values, root-mean-squared deviations, correlation functions, and so on, by
reconstruction of phase portraits which have become widely used quite recently or by calculation
of complicated fractal measures. Additional information, including some features inaccessible for
the direct analysis, can be extracted from time series through
reconstruction of a mathematical model (model equations).
As a rule, real-world signals are complex (often even chaotic), nonstationary, and noisy. The examples
are the recordings from human being obtained with the use of diagnostic devices (see the left Figure:
electric signals from scalp and muscles - electroencephalogram and electromyogram, pressure recordings
from throat and nephron). Processing of such signals requires development and employment of different
methods and tricks (technologies) some of which are classical and used for a long time, while others
appeared recently and currently gain their popularity. For definiteness, one can systematize them
according to their relation to the following two approaches. Observed
time realizations can be analyzed directly, e.g., by computation of classical Fourier spectra
(decomposition into sinusoidal functions) or modern wavelet spectra, by estimation of probability
distribution, mean values, root-mean-squared deviations, correlation functions, and so on, by
reconstruction of phase portraits which have become widely used quite recently or by calculation
of complicated fractal measures. Additional information, including some features inaccessible for
the direct analysis, can be extracted from time series through
reconstruction of a mathematical model (model equations).
2. Investigation of applied possibilities of nonlinear dynamics approaches and, in particular,
methods of empirical model reconstruction.
|
|---|
For a complete characterization of a harmonic signal one must specify its amplitude, initial phase,
and frequency. For more complex, yet regular, signals it is sufficient to perform their decomposition
into sinusoidal functions. Description of a chaotic signal involves such complex and
difficult-to-determine characteristics as, e.g., spectra of dimensions and Lyapunov exponents.
These new characteristics expand possibilities of researchers. However, conditions of their
applicability must be carefully analyzed and the techniques of analysis are expected to be corrected
or modified taking into account specific features of an object and practical goals.
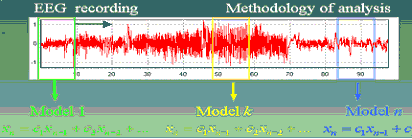 Analogously, one must investigate applicability of an indirect (model-dependent) approach to concrete
goals, situations, and objects. Realization of intriguing promises (validation of the existing ideas
about an object functioning, prediction of the future behavior, signal classification, "measurement"
of something inaccessible for a device, estimation of coupling between different parts of an object
from the recordings of their oscillations) requires efficient mathematical constructions.
Analogously, one must investigate applicability of an indirect (model-dependent) approach to concrete
goals, situations, and objects. Realization of intriguing promises (validation of the existing ideas
about an object functioning, prediction of the future behavior, signal classification, "measurement"
of something inaccessible for a device, estimation of coupling between different parts of an object
from the recordings of their oscillations) requires efficient mathematical constructions.
Examples of applied possibilities of different approaches to
analysis of complex signals and modeling from time series, both known from the literature and
developed by our group, are presented at a separate page
of our cite.
3. Construction and experimental investigation of nonlinear radiophysical systems exhibiting
complex dynamics. Simulation of standard nonlinear models for oscillatory and wave phenomena.
|
|---|
Experimental study of physical models is still an actual problem in physics in spite of grand
development of computers and immense possibilities of numerical investigation of mathematical
models including multi- and infinite-dimensional ones, linear and nonlinear, and impressive
methods of information presentation. A physical model lives according to laws of nature in
contrast to a mathematical model living in accordance with the laws of logics with peculiarities
inherent to computational algorithms. Thus, it is obvious that one needs to verify the results
obtained with discrete models and discrete-time computations in the experimental setups, which
are closer to the real world with its continuous time.
On the other hand, the presence of noise and instabilities often distorts the picture of
processes taken place in the real systems in such a way that it is impossible to understand
this picture without theoretical background. The results of analytical and theoretical
investigation of mathematical models play the role of compass and map in this nonlinear “wood”.
The known rule that effective physical experiment is usually based on some theoretical conception
is especially actual for investigation of the systems with complex and chaotic dynamics,
particularly if they have high dimension.
The descriptions of the laboratory radiophysical schemes examined in our Group and the results
of their nonlinear features investigation are given below.
- Systems with piecewise-linear characteristics
- Analogue and digital systems with time-delayed feedback
- Quasiperiodic driving and SNA
- Experimental implementation of complex maps
- Coupled map lattices
- Fast bifurcations (simulation and physical experiment). Noise generators
|