Dynamical modeling
Before construction of a model, it is important to formulate the requirements to its predictive
abilities. This choice determines the kind of necessary mathematical tools. If precise and unique
forecast of the future states based on the current one is not desired then the probabilistic
approach is traditionally used. Hence, at least some of the quantities describing an object of
modeling are claimed to be random, i.e. unpredictable in principle, stochastic. There can be
different justifications for such a "verdict". If it is "signed", then the tools of the theory of
probabilities and mathematical statistics should be used.
An alternative approach is called "dynamical" and relies on the concept of determinism. Determinism
is the doctrine claiming regularity and causation in all natural and social phenomena. To realize this
approach, one needs mathematical constructions providing a unique forecast. Its classical (but not
unique) exponent are differential equations.
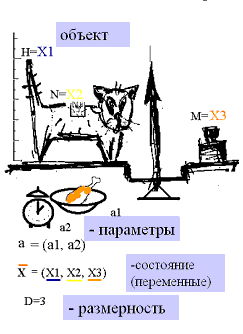
Thus, the dynamical approach is based on the idea that the entire future behavior of an object is
uniquely determined by its state (x) at the initial time instant. The state
(or state vector) is a set of D values: x=(x1, x2, ..., xD);
D is its "dimension". The rule which uniquely determines the object
evolution from the initial state x(t0) is called "evolution operator"
Фt. The state at any future time instant t0+t is found
as x(t0+t)=Фt(x(t0)).
Evolution operator can be specified with the aid of equations,
maps, matrices, graphs, and in other ways, which meet the "unique forecast" condition. The entire model
construction described is called "dynamical system".
|
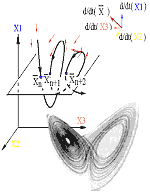
Let us consider an ordinary cat as an example. If the goal of modeling is description of its
health dynamics, one can use the mass M=x3, height H=x2,
and hair density (number of hairs per square unit) N=x1 as dynamical variables.
The set x=(x1, x2, x3) is the state vector; the
dimension is D = 3. We cannot derive an expression for the evolution operator, but it is
obvious that cat development depends, e.g., on its food (a1 - mass of the food per a
day, kg/day) and life conditions (a2 - duration of walks per a day, hour/day).
In contract to dynamical variables, the quantities a1, a2 and similar
to them (which can be held constant or controlled) are called "parameters". Coefficients in
evolution equations are parameters of dynamical systems.
|
Separation of characterizing quantities into variables and parameters is dictated by
the formulation of the modeling problem. If the goal of modeling of the cat were description
of its mechanical movement in space (rather than health), it would be logical to take
coordinate of its mass center (x1=x, x2=y, x3=z) and Euler
angles of its "longitudinal axis" (x4=α, x5=β, x6=γ)
as dynamical variables, while its mass M, downiness N and size H which are
constant during a jump but influence the "flight" should be considered as parameters
(a1=M, a2=>N, a3=H). Note that the
quantities serving as dynamical variables in one problem setting turned into parameters for the other.
|
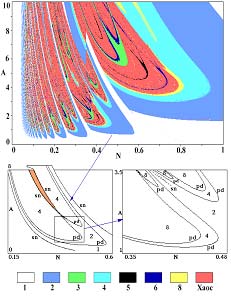
Dynamical modeling suggests very wide possibilities of visualization of information, e.g.,
portraits in state space (see Figures) - phase portraits, representation of the parameters space
as a chart showing the regions where different kinds of motions exist, etc.
|